목차
> 신경망 학습 원리: 경사 하강법
기울기 소실 문제(Vanishing Gradient Problem)
> 연속형 활성 함수를 사용하는 이유
> 기울기 소실 문제의 원인 : 구조적인 문제
> 첫 번째 해결 방법: 활성 함수를 변경하기
> 두 번째 해결 방법: 신경망의 구조 변경하기
오늘은 인공 지능의 2차 혹한기(AI Winter)를 초래한 기울기 소실(Vanishing Gradient) 문제의 정의와 이를 해결하기 위한 노력들에 대해 알아보도록 하겠습니다.
■ 인공 신경망은 어떻게 학습하는 걸까?
신경망 학습: 경사 하강법(Gradient Descent), 산의 꼭대기에서 눈을 감고 하산하다.

기울기 소실(Vanishing Gradient) 문제를 이해하기 위해서는 먼저 인공 신경망이 어떻게 학습하는지를 알아야 합니다. 인공 신경망은 노드와 노드 간 연결이 겹겹이 쌓인 구조입니다. 연결의 세기를 가중치(Weight)라고 하며, 인공 신경망의 학습은 끊임없는 수학적 연산을 통해 가중치를 최적 값으로 갱신하는 과정입니다.
이때, 가중치를 갱신하는 기준이 필요한데요. 이 기준은 목적 함수(Object Function)를 통해 정의합니다. 목적 함수는 인공 신경망 내의 파마리터(가중치와 Bias 등)로 이루어진 다차원 방정식입니다.
일반적으로 목적 함수를 '최소화'하는 방식으로 신경망의 가중치가 갱신됩니다. 목적 함수는 고차원 방정식이어서 그래프로 표현하면 <그림 1>과 같은데요. 이와 같은 고차원 방정식은 어떤 파라미터를 움직여야 함수의 값을 줄일 수 있는지에 대해 알기 어렵습니다.
이때, 어떤 파라미터를 조정할지에 대한 기준을 정하기 위해 기울기 하강(Gradient Descent) 방식을 사용합니다.
기울기 하강이란, 눈을 감고 산 정상에서 하산하는 것과 같은 방식입니다. 눈을 감으면, 방향을 알 수 없기 때문에 현재 자신의 위치에서 360도 발을 디디며 경사가 낮은 곳을 탐색합니다. 그리고 가장 낮은 경사를 향해 한 발자국 내딛고 이 과정을 반복합니다.
이를 목적 함수에 적용해 보겠습니다. 현재 위치에서, 경사가 낮은 방향을 확인하기 위해 미분을 구합니다. 고차원 방정식이므로, 이 미분 값은 각 변수들의 편미분으로 구성되고 편미분의 집합을 그레디언트(Gradient)라고 합니다.
경사가 낮은 곳을 향해 한 발자국 내딛는 것은 비용 함수의 그레디언트가 가장 낮아지는 방향(하강, Descent)을 향해 각 축의 값(파라미터, 가중치와 편향)을 조절하는 것과 동일합니다. 이런 방식으로 가중치 등은 오차가 작아지도록 갱신(학습) 됩니다.
▶ 참고자료 : 그레디언트(Gradient)의 정의 https://ko.wikipedia.org/wiki/%EA%B8%B0%EC%9A%B8%EA%B8%B0_(%EB%B2%A1%ED%84%B0)
기울기 (벡터) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 물매는 여기로 연결됩니다. 무기에 대해서는 무릿매 문서를 참고하십시오. 위의 두 그림에서는 회색의 밝기가 스칼라계의 크기를 뜻한다. 짙은 색일수록 크기
ko.wikipedia.org
■ 기울기 소실 문제(Vanishing Gradient Problem)
기울기 소실: 인공 신경망이 깊어질수록, 학습이 안 되는 모순

기울기 소실이란 인공 신경망의 가중치 갱신을 위해 전달되는 오차 정보가 0으로 수렴하여 학습이 전혀 진행되지 않는 상태를 의미합니다.
자세히 살펴보겠습니다. <그림 2>의 왼쪽 그림은 깊은 인공 신경망(Deep Neural Network)의 예시입니다. 수많은 노드와 가중치가 있기 때문에, 이들을 모두 갱신시키기 위해 오차의 값을 출력층에서 입력층으로 거꾸로 흘려보내며 가중치를 갱신합니다.
이를 오류 역전파(Back-Propagation)라고 합니다. 역전파 과정은 출력층에서 입력층으로 층을 내려갈수록 활성화 함수의 편미분 값이 계속 곱해지는 구조입니다. 기울기 소실 문제는 이 구조적인 문제로 발생합니다.
과거 인공 지능 분야에서는 활성화 함수로 시그모이드(Sigmoid) 함수를 많이 사용했습니다. 활성화 함수를 사용한 이유는 인간의 학습을 모방하기 위해서입니다.
최초의 인공 신경망인 퍼셉트론(Perceptron)은 일정 역치가 넘으면 신호를 흘리고, 역치 이하이면 신호를 전달하지 않는 불연속적 구조입니다.
반면, 인간의 학습은 점진적이고 연속적입니다. 오랜 시간에 걸쳐 지식을 습득합니다. 인공 신경망은 이러한 인간의 점진적 학습을 모방하기 위해 연속적인 활성화 함수를 도입했습니다.
그리고 이때, 가장 많이 활용된 연속적인 활성 함수가 시그모이드 함수입니다.
그렇다면 도대체 구조적인 문제가 뭐야?
본론으로 돌아와서, 기울기 소실 문제에 대해 다시 살펴보겠습니다. <그림 2>의 오른쪽 그래프는 시그 모이드 함수의 그래프입니다. 앞서, 편미분은 기울기라고 말씀드렸습니다.
활성화 함수의 그래프를 보시면 거의 대부분 영역에서 기울기가 0에 가까우며, 학습이 용이한 영역(기울기가 어느 정도 보장된 영역)은 그리 넓지 않습니다.
오류 역전파는 층을 거칠수록 활성화 함수의 편미분이 계속 곱해지는 구조인데, 곱해지는 값이 0 또는 굉장히 작은 수일 확률이 높으니 결과적으로 망이 깊어질수록(층이 많아질수록) 역전파 되는 오차의 값이 0에 수렴하여 가중치 갱신이 이루어지지 않게 됩니다.
요약하면, 망이 깊어질수록 인공 신경망의 학습이 되지 않는 것입니다. 복잡한 현실의 문제를 해결하기 위해서는 깊은 인공 신경망(Deep Neural Network)이 필요하지만, 인공 신경망이 깊어질수록 학습이 안 되는 모순적인 상황. 인공 지능 분야는 이런 모순적인 상황 속에 좌절하고, 2차 암흑기(AI Winter)를 겪게 됩니다.
■ 기울기 소멸(Vanishing Gradient)을 해결하기 위한 다양한 방법들
미션: 오차를 입력층까지 손실 없이 전달하라!
이제 여러분은 기울기 소멸 문제가 오차를 입력층으로 역전파 할수록 오차가 0으로 수렴한다는 인공 신경망의 구조적인 문제로 인해 발생하는 것임을 알게 되었습니다.
이러한 문제는 어떻게 해결할 수 있을까요? 핵심은 명확합니다. 오차를 입력층까지 손실 없이 잘 전달한다면 기울기 소멸 문제는 해결됩니다.
다행히 오늘날에는 이러한 문제를 해결하기 위한 다양한 방법론이 존재합니다. 크게 두 가지 접근 방식이 있습니다. 첫 번째는 활성화 함수를 바꾸는 것, 두 번째는 인공 신경망의 구조를 바꾸는 것입니다.
첫 번째 해결방법: 활성화 함수를 바꿔라
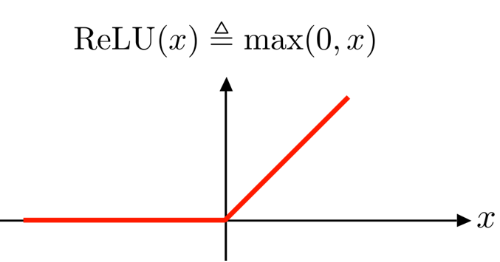
현대 인공 신경망 분야를 공부한다면 ReLU 함수에 대해 한 번씩은 들어보셨을 겁니다.
ReLU 함수는 굉장히 간단한 구조의 함수입니다. 0보다 작은 값이 들어오면, 0을 출력하고 0보다 큰 값이 들어오면 들어온 값 그대로 출력합니다.
인공 신경망의 활성화 함수로 시그모이드 대신 ReLU를 사용하면 크게 세 가지의 장점이 있습니다.
첫 째, 시그모이드 함수보다 기울기 소멸 문제가 발생할 확률이 현격히 낮습니다.
시그모이드 함수는 0에서 1 사이의 값만 취하지만, ReLU 함수는 0에서 무한대 사이의 값을 출력합니다. 물론, 학습의 발산을 방지하기 위해 일반적으로 많은 논문에서 6 이하의 값만 출력하도록 제한하기도 합니다.) 따라서 오차가 역전파 될 때, 0보다 큰 값이 곱해질 확률이 높아서 기울기 소멸 가능성이 줄어듭니다.
둘째, 시그모이드 함수보다 계산량이 크게 감소합니다.
시그모이드 함수는 지수가 포함된 분수 함수이지만 ReLU함수는 0보다 큰 상태에서 직선의 함수입니다. 미분값을 계산할 때, 시그모이드 대비 ReLU 함수의 계산량이 압도적으로 작습니다. 이 계산량의 차이는 신경망이 깊을수록 커집니다.
셋째, 웬만한 경우에 시그모이드 함수보다 ReLU 함수를 사용하는 인공 신경망이 더 잘 동작합니다.
여기에는 다양한 해석이 있습니다. ReLU 함수의 구조 자체가 굉장히 간단하기 때문에, 깊은 망을 쌓을 수 있고 이러한 방식이 마치 앙상블(ensemble) 학습처럼 작용한다는 해석도 있습니다.
ReLU 이외에도 tanh 함수나 ReLU 함수를 살짝 변형한 Leakyed ReLU함수 등이 있습니다. 현대 인공 신경망은 대부분 ReLU를 사용하거나 ReLU를 살짝씩 변형한 ReLU 계열의 함수를 기본 활성화 함수로 사용하고 있습니다.
두 번째 해결방법: 인공 신경망의 구조를 바꿔라
눈을 감고, 인공 신경망을 떠올려보겠습니다. 흔히 알고 있는 인공 신경망은 각 층에 노드가 있고, 노드들이 순차적으로 연결된 구조입니다.
하지만, 이런 구조는 신경망이 깊어질수록 기울기 소실 문제에서 벗어나기 어렵습니다. 입력층까지 오차가 전달되기 위해 거쳐야 하는 스텝이 많을뿐더러, 가중치가 작은 신경망이라면 학습이 잘 되지 않기 때문입니다.
이러한 구조를 탈피하기 위해 정보 고속도로(Information Highway)의 개념이 인공 신경망에 활용되었습니다. 정보 고속도로는 통신 분야에서 자주 인용되는 개념인데요. 인공 신경망에 영감을 준 개념은 정보(오차 등)를 멀리 떨어진 노드로 바로 전달하는 개념입니다.
정보 고속도로가 최초로 적용된 인공 신경망은 CNN(Convolution Neural Network)의 ResNet(Residual Neural Network)입니다.
ResNet에는 데이터가 흐르는 Path와 활성화 함수가 없는 Path가 따로 있습니다. 이를 Skip Connection이라고 하는데요. 활성화 함수가 없는 Path로 오차가 흐르기 때문에, 망이 깊어도 Vanishing 문제가 발생하지 않습니다.
'AI - Deep Learning' 카테고리의 다른 글
| 활성화 함수: 정의와 종류, 비선형 함수를 사용해야 하는 이유 (0) | 2022.11.01 |
|---|---|
| 딥 러닝을 위한 회귀 분석의 이해: Logit, Sigmoid, Softmax (5) | 2022.10.31 |
| 인공지능(AI) 배경지식: 용어의 유래부터 현재의 딥러닝(DNN)까지 (2) | 2022.10.14 |
| 최초의 신경망 모델 퍼셉트론: 정의, 동작 원리 그리고 한계점 (2) | 2022.10.11 |
| 논리 연산의 그래프적인 해석과 Python 코드 (0) | 2022.10.10 |




댓글