안녕하세요! 모두의 IT부케, 케빈입니다.
오늘은 Python으로 논리 연산을 구현하는 시간을 가져보겠습니다.
■ 논리 연산과 논리 회로(게이트)
논리 연산(logical operation): 참과 거짓의 연산 & 논리 회로(logic gate): 논리 연산의 물리적 구현
학창 시절, True(1)와 False(0)의 연산을 배우신 기억이 나시나요? 우리는 이를 논리 연산(logical operation)이라고 부릅니다. 다른 말로 불 연산(Boolean expression)이라고도 하는데요. 이러한 불 연산은 컴퓨터 공학이나 전자 공학(또는 반도체)에 많이 활용되고는 합니다. 불 연산 또는 불 대수를 물리적 장치에 구현한 것이 바로 논리 회로(logic gate), 즉 논리 게이트라고 할 수 있습니다. (논리 회로와 논리 게이트는 거의 동일한 말로 사용됩니다.)
논리 연산을 분류(Classification)의 문제와 연관 지어서 해석하는 것은 퍼셉트론(Perceptron) 이론을 보다 깊게 이해하는데 도움이 됩니다. 심도 깊은 학습을 위해 오늘은 기본 논리 연산인 AND, NOT, OR, XOR에 대해 알아보도록 하겠습니다.
관련 내용은 밑바탕부터 배우는 딥러닝이라는 교재를 참고하였으며, 논리 회로(logic gate)는 기회가 된다면 반도체 코너에서 따로 다루도록 하겠습니다.
■ 논리곱 연산(AND)의 그래프적 해석과 Python 코드
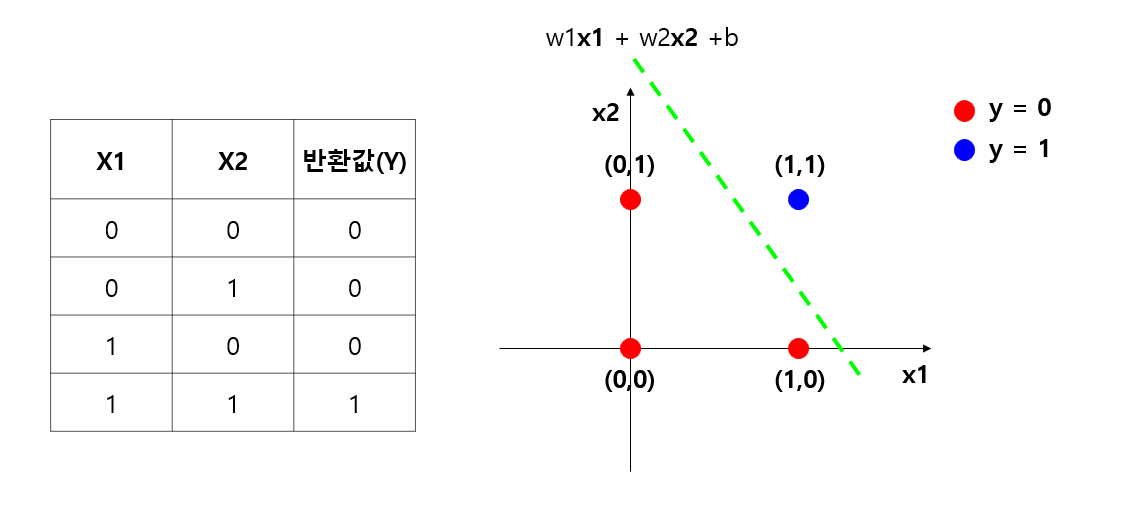
위 사진은 논리곱(AND)의 진리표(Truth Table)입니다. 논리곱은 두 명제 또는 두 입력값(x1, x2)이 모두 참이어야 참 값을 돌려주는 연산입니다. 이러한 특성 때문에 논리곱이라고 불립니다. 위 사진을 보면, 왼쪽의 진리표(Truth Table)에 대한 결과값을 x1과 x2를 각각 축으로 삼는 2차원 그래프로 표현할 수 있습니다. 이러한 표현은 0 또는 1의 값만 갖는 반환값(y)의 이진 분류(Classification)로 해석하는 것과 동일합니다.
자, 위 그림에서 우리는 빨간색 점과 파란색 점을 구별할 수 있는 임의의 선을 그을 수 있습니다. 그 선을 w1x1 + w2x2 + b라고 수학적으로 표현할 수 있습니다. (x1과 x2 차원의 임의의 직선이니까요.) 직선의 값보다 작은 영역은 0으로, 큰 영역은 1로 정의한다면 논리 연산은 2차원 평면에서 임의의 직선으로 이진 분류를 할 수 있는 선형 문제가 되는 것입니다. 이를 Python 코드로 구현하면 아래와 같습니다.
def AND(x1,x2):
w1,w2,theta = 0.5,0.5,0.7
line = w1*x1+w2*x2 # 직선의 방정식, w1x1 + w2x2
if line > theta:
print(True)
else:
print(False)
def AND_with_bais(x1,x2):
w1,w2,b = 0.5, 0.5, -0.7
line = w1*x1+w2*x2 + b
if line > 0:
print(True)
else:
print(False)
for x1 in [0,1]:
for x2 in [0,1]:
print("====\n",x1,x2)
AND(x1,x2)
#AND_with_bais(x1,x2)# AND 결과값
====
0 0
False
====
0 1
False
====
1 0
False
====
1 1
True위 공식에서 w1, w2, theta 값은 임의의 값입니다. 빨간색과 파란색 점을 구분할 수 있으면 되기 때문에, 값의 조합은 무한대이며 가장 편한 숫자를 사용했습니다. w1*x1 + w2*x2 직선에 값을 (x1, x2) 값을 대입했을 때, 0.7보다 크면 1이고 작으면 0으로 분류(Classification)하는 내용입니다. 이때, 0.7(=theta)를 우변으로 넘기고 bias로 정의한 함수가 AND_with_bias인데 근본적으로 두 함수는 동일하지만 bias가 있는 함수가 더 퍼셉트론(Perceptron)에 가까운 표현 방식이라고 생각하시면 됩니다.
■ 부정 논리곱 연산(NAND)

논리곱(AND)을 이해하셨다면, 부정 논리곱(NAND) 연산은 자동으로 이해하신 겁니다. NAND는 Not AND의 합성어로, 부정 논리곱(NAND) 연산은 AND의 정반대 값을 반환합니다. 다시 말해, 두 명제 또는 두 입력값이 모두 거짓일 경우에만 거짓을 반환하고 나머지는 참값을 반환합니다. 위 AND 연산에서 0.7보다 큰 값을 1로 설정했으므로, NAND에서는 0.7보다 작은 값을 1로 정의해줍니다. Python 코드도 AND에서 부호만 바꿔주면 NAND 연산이 됩니다.
def NAND(x1,x2):
w1,w2,theta = -0.5,-0.5,-0.7
line = w1*x1+w2*x2 # 직선의 방정식, w1x1 + w2x2
if line > theta:
print(True)
else:
print(False)
def NAND_with_bais(x1,x2):
w1,w2,b = -0.5, -0.5, 0.7
line = w1*x1+w2*x2 + b
if line > 0:
print(True)
else:
print(False)
for x1 in [0,1]:
for x2 in [0,1]:
print("====\n",x1,x2)
NAND(x1,x2)
#NAND_with_bais(x1,x2)#NAND 결과값
====
0 0
True
====
0 1
True
====
1 0
True
====
1 1
False
■ 논리합 연산(OR)

이번에는 논리합 연산(OR)을 살펴보겠습니다. 논리합은 두 명제 또는 두 입력값(x1, x2) 중 하나만 참이어도 참값을 반환합니다. 마찬가지로 x1과 x2의 2차원 평면에서 반환값(0과 1)을 분류하는 이진 분류(Classification) 문제로 해석하여 그래프로 표현할 수 있습니다. 이번에도 빨간색 점과 파란색 점을 구별하는 직선을 찾는 것은 어렵지 않아 보입니다. Python 코드는 아래와 같이 구현할 수 있습니다.
def OR(x1,x2):
w1,w2,theta = 0.5,0.5,0.2
line = w1*x1+w2*x2 # 직선의 방정식, w1x1 + w2x2
if line > theta:
print(True)
else:
print(False)
def OR_with_bais(x1,x2):
w1,w2,b = -0.5, -0.5, 0.2
line = w1*x1+w2*x2 + b
if line > 0:
print(True)
else:
print(False)
for x1 in [0,1]:
for x2 in [0,1]:
print("====\n",x1,x2)
OR(x1,x2)
#OR_with_bais(x1,x2)# OR 결과값
====
0 0
False
====
0 1
True
====
1 0
True
====
1 1
Trueline의 기울기(w1, w2) 값을 바꾸지 않고 theta 값만 바꿔도(평행 이동) 충분히 OR 연산을 구현할 수 있습니다.
■ 배타적 논리합 연산(XOR)

대망의 배타적 논리합(XOR) 연산이 왔습니다. 배타적 논리합 연산은 두 명제 또는 입력값(x1, x2) 중 정확히 하나만 참이거나 두 명제 또는 입력값의 참 거짓 여부가 다를 때만 참값을 반환합니다. 이를 그래프로 표현하면 위 그림과 같은데요. 만약 여러분께서 배타적 논리합(XOR)의 2차원 그래프에서 파란색 점과 빨간색 점을 정확히 구분할 수 있는 직선을 그릴 수 있다면, 축하드립니다. 당신은 천재입니다.
배타적 논리합(XOR)은 2차원 그래프에서는 두 점을 완벽하게 분류할 수 없습니다. 3차원(z축)에서는 가능하겠지만요. 따라서, 이 문제는 선형 분류가 아닌 비선형 분류에 해당됩니다. 계속 설명드린 논리 연산의 그래프적인 해석은 퍼셉트론에 근거한 해석 방식입니다. 그리고 위 배타적 논리합의 예시는 최초의 인공 신경망인 퍼셉트론이 기초적인 논리 연산도 풀 수 없다, 그리고 궁극적으로 비선형 문제를 풀 수 없다는 증거입니다. 이러한 사실 때문에 초창기 인공 지능 분야는 연구 지원과 관심이 사라져 버리는 혹한기(AI Winter)를 보내기도 합니다.
배타적 논리합(XOR)도 마찬가지로 Python 코드로 나타낼 수 있습니다. 단, 비선형 문제이기 때문에 선형 함수를 여러 번 중첩(Layer 방식)하여 구현해야 합니다. 아래 그림은 NAND, OR, AND Gate를 중첩하여 XOR Gate를 구현한 내용입니다. 아래 논리 회로도를 토대로 Python 코드를 작성하겠습니다.

입력값(x1, x2)은 NAND와 OR 연산을 각각 통과해야 하며, 통과된 두 개의 연산 값(NAND와 OR의 결과값)이 AND 연산에 입력값(z1, z2)으로 들어가면 됩니다.
def AND(x1,x2):
w1,w2,theta = 0.5,0.5,0.7
line = w1*x1+w2*x2
if line > theta:
return True
else:
return False
def NAND(x1,x2):
w1,w2,theta = -0.5,-0.5,-0.7
line = w1*x1+w2*x2
if line > theta:
return True
else:
return False
def OR(x1,x2):
w1,w2,theta = 0.5,0.5,0.2
line = w1*x1+w2*x2
if line > theta:
return True
else:
return False
def XOR(x1,x2):
z1 = NAND(x1,x2)
z2 = OR(x1,x2)
y = AND(z1,z2)
print(y)
for x1 in [0,1]:
for x2 in [0,1]:
print("====\n",x1,x2)
XOR(x1,x2)# XOR 결과값
====
0 0
False
====
0 1
True
====
1 0
True
====
1 1
False
오늘은 논리 연산에 대해 알아봤습니다. 궁금한 내용이나 오류가 있다면 댓글로 남겨주세요.
긴 글, 읽어주셔서 감사합니다. :)
'AI - Deep Learning' 카테고리의 다른 글
| 활성화 함수: 정의와 종류, 비선형 함수를 사용해야 하는 이유 (0) | 2022.11.01 |
|---|---|
| 딥 러닝을 위한 회귀 분석의 이해: Logit, Sigmoid, Softmax (5) | 2022.10.31 |
| 인공지능(AI) 배경지식: 용어의 유래부터 현재의 딥러닝(DNN)까지 (2) | 2022.10.14 |
| 인공 신경망 학습 원리와 기울기 소실 문제 정의 및 해결법 한 글로 정리 (1) | 2022.10.13 |
| 최초의 신경망 모델 퍼셉트론: 정의, 동작 원리 그리고 한계점 (2) | 2022.10.11 |




댓글